Diagrama de árbol

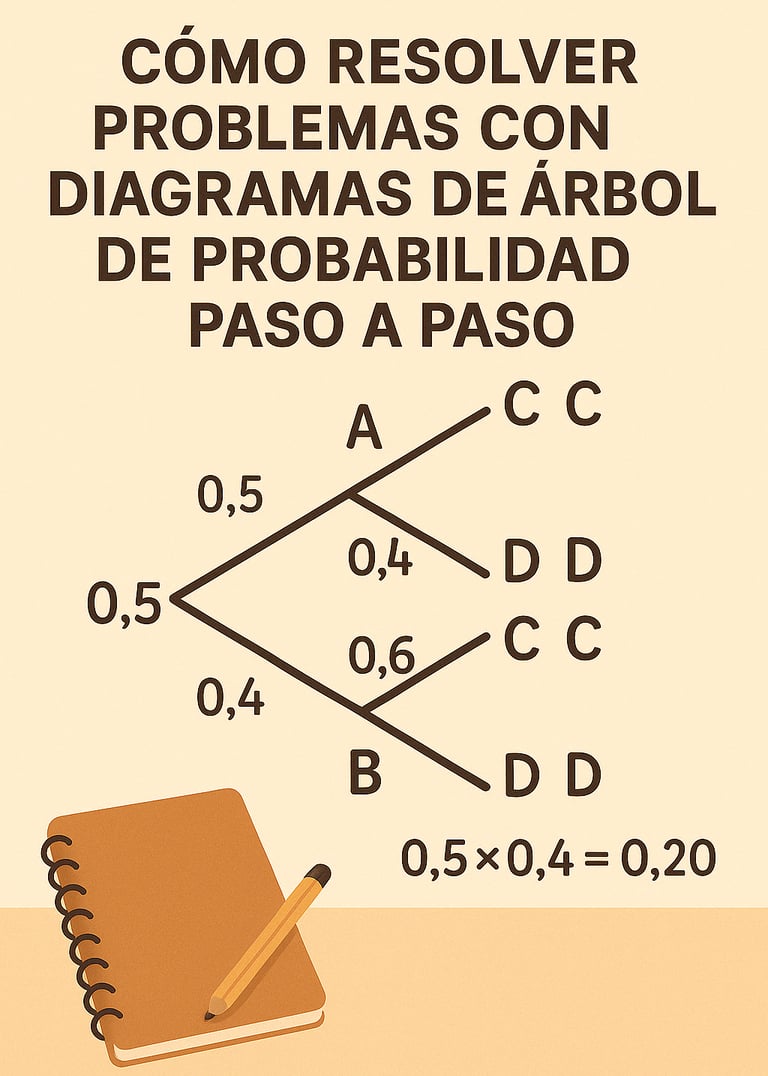
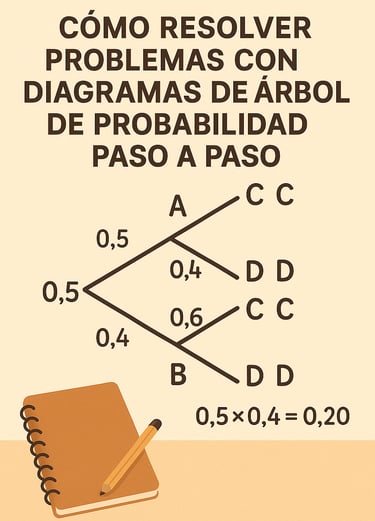
Ejemplo resuelto

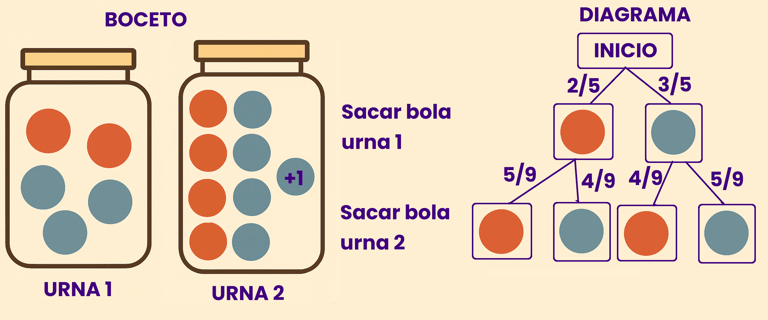
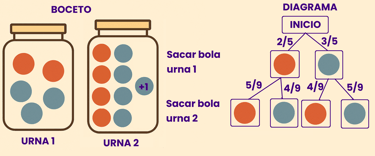
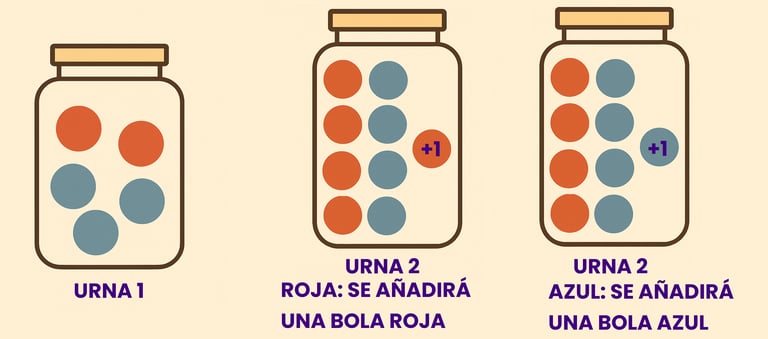
En una habitación hay 2 urnas. En la urna numero 1 hay 2 bolas rojas y 3 bolas azules. En la urna numero 2 hay 4 bolas rojas y 4 bolas azules. Se saca una bola al azar de la urna 1 y se deposita en la urna numero 2. A continuación se extrae una bola de la urna numero 2 y se comprueban las distintas probabilidades

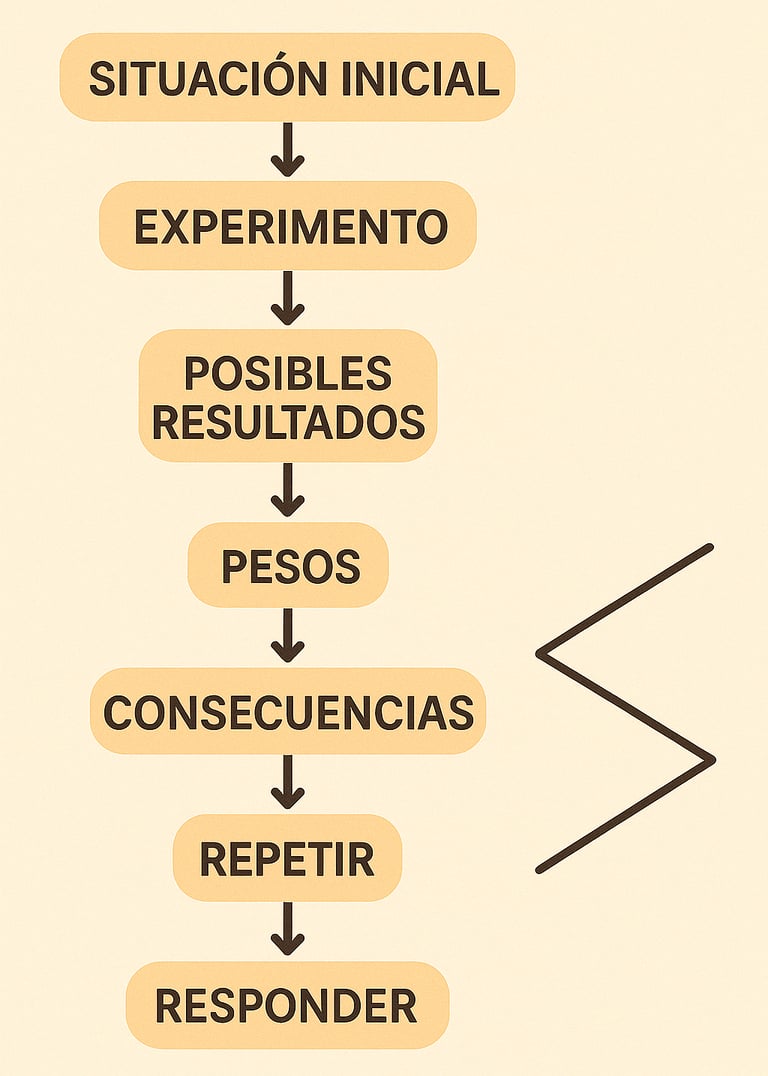
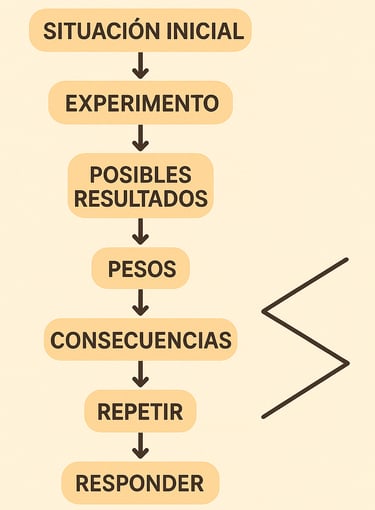
Paso - 1 (SITUACIÓN INICIAL)

En la situación inicial debemos leer el problema e imaginarnos la situación, es decir, tener una idea mental de la situación que nos están planteando.

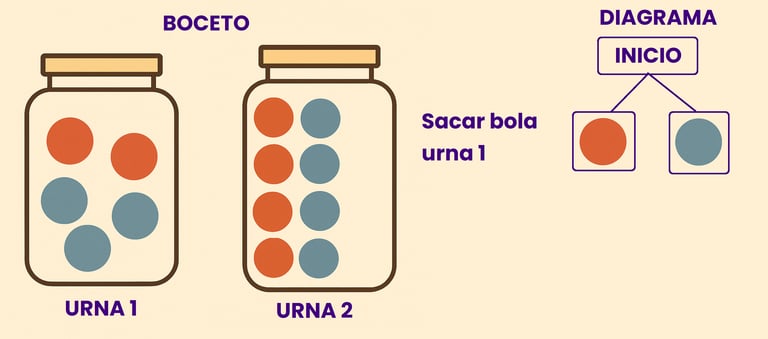
En este problema sabemos que lo primero que vamos a realizar es algún tipo de acción sobre la urna numero 1, y posteriormente sobre urna numero 2. En esta etapa también suele ser interesante hacerse un pequeño boceto , que permita tener una idea visual del problema, por ejemplo , dibujar ambas urnas.

La situación inicial se suele representar como un circulo en blanco desde donde empezará a crecer el árbol que vamos a establecer

Paso - 2 (EXPERIMENTO)

El siguiente paso, es detectar cual es el primer experimento o el primer suceso que ocurre dentro del problema. Una vez reconocido, que a veces es un poco complicado porque no tiene porque ser en el mismo orden en el que el ejercicio está escrito. Analizamos dicho experimento, en este caso sacar una bola de la urna numero 1.

Paso - 3 (POSIBLES RESULTADOS)

El tercer paso es escribir todos los posibles resultados que puedan obtenerse del experimento. En el caso de sacar 1 bola de la urna numero 1 solo pueden suceder 2 cosas. O que la bola sea roja o que sea azul. Y una vez plasmados dibujamos una línea que una esos resultados con la situación anterior, en este caso con la casilla inicio.

Paso - 4 (PESOS)

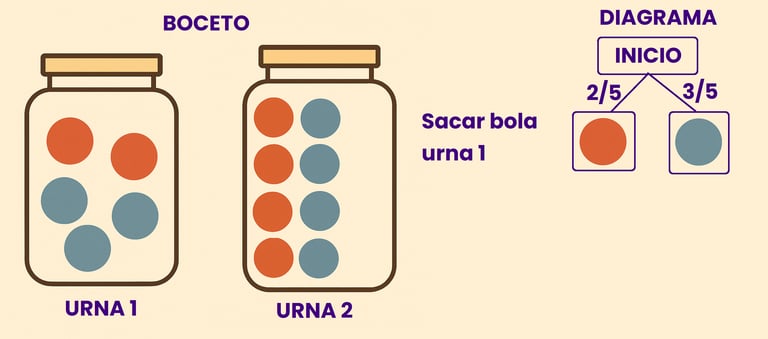
Se le llama peso a la probabilidad de que suceda un suceso u otro. Normalmente dicha probabilidad se calcula mediante los casos favorables dividido los casos posibles la otra opción es que el propio problema ya nos diga la probabilidad en forma de fracción o de porcentaje. En este caso nos fijamos en el primer posible resultado que es obtener una bola roja. Si nos fijamos en la urna 1, la probabilidad de sacar una bola roja es 2/5, porque los casos favorable, es decir, el numero de bolas que cumplen esa condición son 2, dividido de los caso posibles, es decir, el numero total de bolas que hay que son 5, por eso es 2/5. De la misma forma la probabilidad de sacar una azul es 3/5.

Anotamos esos resultados en las líneas que unen los resultados con el suceso anterior. Nótese que la suma de los pesos del mismo nivel siempre tiene que sumar 1 (2/5 + 3/5 = 5/5 =1 )

Paso - 5 (CONSECUENCIAS)

A veces, no siempre, el evento del experimento 1 tiene consecuencias para el experimento 2. En este caso el que haya salido una bola roja o azul en la urna 1 si tiene consecuencias porque la bola que se depositará en la urna 2 dependerá del color que haya salido al extraerla. Si salió roja, se depositará en la urna 2 y la urna 2 pasará a tener 5 bolas rojas y 4 azules. Y si salió azul, habrá 5 bolas azules y 4 rojas. Hay que tener esto en cuenta a la hora de analizar el experimento siguiente.

Paso - 6 (REPETIR)

Hay que volver a repetir los pasos 2,3,4 y 5 hasta que todos los experimentos hayan quedado plasmados en el diagrama de árbol.

En nuestro caso ahora sacamos una bola de la urna 2, teniendo en cuenta las consecuencias del anterior experimento. Empezamos por la rama de la bola roja.

Como en la primera extracción sacamos 1 bola roja, ahora en la urna 2 hay 5 bolas rojas y 4 azules.. Apuntamos que los posibles resultados es bola roja y bola azul y que los pesos son. 5/9 de sacar una bola roja y 4/9 de sacar una azul, que efectivamente entre las 2 ramas suman 1

Paso - 7 (RESPONDER)

A partir de este punto ya tenemos el diagrama establecido por lo que ya podemos contestar a las preguntas que nos realiza el ejercicio aquí hay una pequeña selección de preguntas que pueden hacernos y como contestarlas

¿Cuál es la probabilidad de sacar una bola roja de la urna 1? P(R1)

Si observamos el primer peso que sale desde el inicio hacia sacar bola de la urna 1 de color rojo, el peso es 2/5, por lo que la probabilidad es de 2/5, es decir, 40%

¿Cuál es la probabilidad de sacar una bola azul de la urna 1? P(A1)

Si observamos el primer peso que sale desde el inicio hacia sacar bola de la urna 1 de color azul, el peso es 3/5, por lo que la probabilidad es de 3/5, es decir, 60%

¿Cuál es la probabilidad de sacar una bola roja de la urna 2? P(R2)

Si observamos veremos que hay 2 posibilidades de sacar una bola roja de la urna 2, o bien, sacamos una bola roja después de haber sacado una bola roja de la primera urna, es decir, el primer camino, o bien, podemos sacar una bola roja de la urna 2 después de haber sacado un bola azul de la primera urna, es decir, camino 3. Puesto que hay 2 posibles caminos para conseguir una bola roja en la extracción de la bola de la urna 2, es lógico pensar que la probabilidad total será la suma de ambas probabilidades.

P(R2)=P(R2|R1) · P(R1) +P(R2|A1) · P(A1)

Ésta fórmula quiere decir que la probabilidad de sacar una bola roja de la segunda urna es igual a la probabilidad de sacar una bola roja de la urna 2 sabiendo que anteriormente habíamos sacado una bola roja de la urna 1 multiplicado por la probabilidad de sacar la bola roja de la urna 1 mas la probabilidad de sacar una bola de roja de la urna 2 sabiendo que habíamos sacado una bola azul de la urna 1 multiplicado por la probabilidad de sacar una bola azul de la urna 1.

P(R2)=P(R2|R1) · P(R1) +P(R2|A1) · P(A1)

P(R2)=[(5/9) · (2/5)] + [(4/9) · (3/5)]=[10/45]+[12/45]=22/45=48.88%

¿Cuál es la probabilidad de sacar una bola azul de la urna 2? P(A2)

Podemos hacer el mismo procedimiento que hemos hecho en la anterior pregunta pero esta vez con los caminos 2 y 4, que corresponden a la segunda bola azul. No obstante hay un método mas rápido ya que como hemos visto cual es la probabilidad de que sea roja, la azul es la probabilidad contraria

P(A2)=1-P(R2)=1-[22/45]=23/45=51.12%

¿Cuál es la probabilidad de sacar una bola roja de la urna 2 y también en la roja 1? P(R2∩R1)

La probabilidad de que se den ambos sucesos es la probabilidad del camino 1, igual que hemos calculado antes

P(R2∩R1)=P(R2|R1) · P(R1)=[(5/9) · (2/5)]=10/45=22.22%

¿Cuál es la probabilidad de que alguna de las 2 bolas sea azul? P(Alguna azul)

La probabilidad de que se alguna bola sea azul, es la probabilidad del camino 2, el camino 3 y 4. Pero para ahorrarnos cálculos, como ya hemos visto cual es la probabilidad de que salgan las 2 rojas, es tan fácil como calcular el contrario.

P(Alguna azul)=1-P(R2∩R1)=1-(10/45)=35/45=77.78%

¿Cuál es la probabilidad de que sabiendo que sabiendo que la segunda bola era roja, que la primera fuera azul? P(A1|R2)

La probabilidad de que la primera bola fuera azul si sabemos que la segunda bola es roja se calcula de la siguiente manera. Puesto que nos están preguntando por un suceso de la primera ramificación y no de la segunda debemos de intercambiar las condiciones puesto que no hay forma de a simple vista calcular dicha probabilidad. Al cambiar el orden de las condiciones, habrá que multiplicarlo por la probabilidad de que la primera bola sea azul y dividirlo por la probabilidad de que la segunda bola sea roja

P(A1|R2)=(P(R2|A1) · P(A1))/P(R2)

P(A1|R2)=(4/9) · (3/5) / (22/45) LA PROBABILIDAD DE R2 YA LA HABIAMOS CALCULADO ANTERIORMENTE

P(A1|R2)=(12/45) / (22/45)

P(A1|R2)=12/22=54.54%

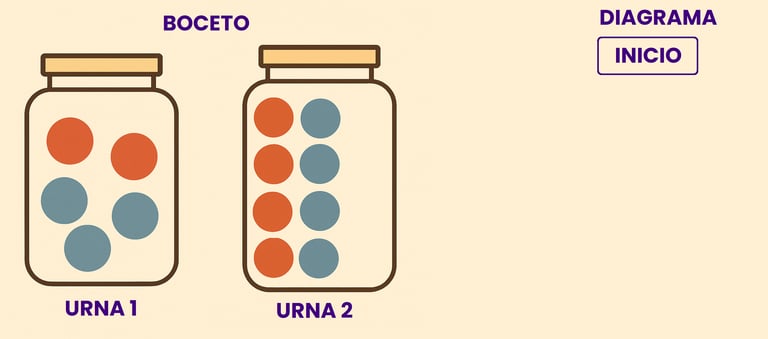
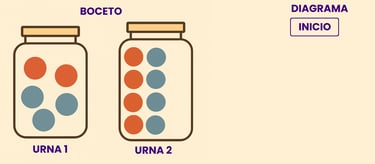
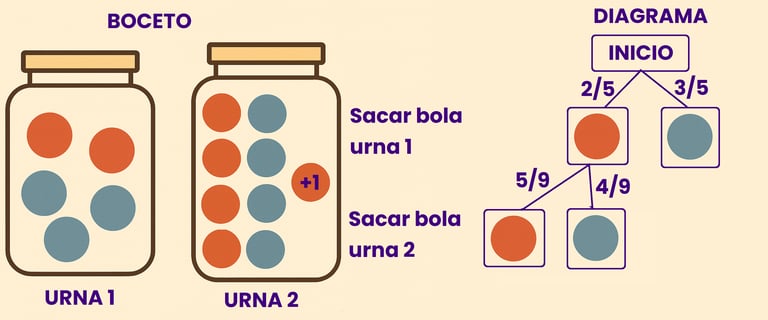
Ahora nos fijamos en la primera extracción de la bola en azul. Como en la primera extracción sacamos 1 bola azul, ahora en la urna 2 hay 4 bolas rojas y 5 azules.. Apuntamos que los posibles resultados es bola roja y bola azul y que los pesos son. 4/9 de sacar una bola roja y 5/9 de sacar una azul, que efectivamente entre las 2 ramas suman 1