Diagrama de Venn

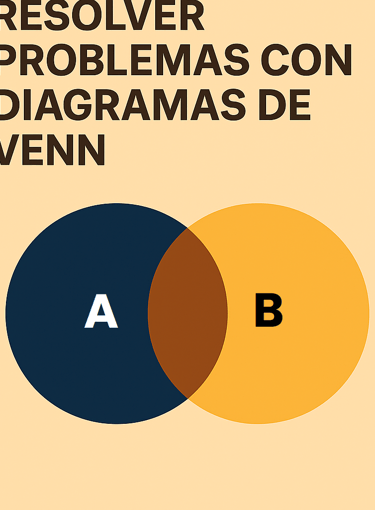
DIAGRAMA DE VENN

Para resolver este tipo de problemas y para la correcta interpretación de ésta explicación primero vamos a definir el gráfico de Venn. El gráfico muestra la probabilidad de 2 sucesos, el suceso A y el suceso B, y si existe algún tipo de compatibilidad entre ambas probabilidades. Para nuestro ejemplo utilizaremos un diagrama de tan solo 2 elementos.

PARTES DEL DIAGRAMA

El diagrama que vamos a representar se compone de de 4 partes:

• La primera parte es A: Que está compuesto por todo el conjunto de A. (rojo)

• La segunda parte es B: Que está compuesto por todo el conjunto de B. (azul)

• La tercera parte es A ∩ B: Que está compuesto por todo el conjunto de A que es también B.

• La cuarta parte es región exterior: Que está compuesto por todo el todo lo que no es ni A ni B. (morado)

DEFINICIÓN DE REGIONES

UNIÓN E INTERSECCIÓN

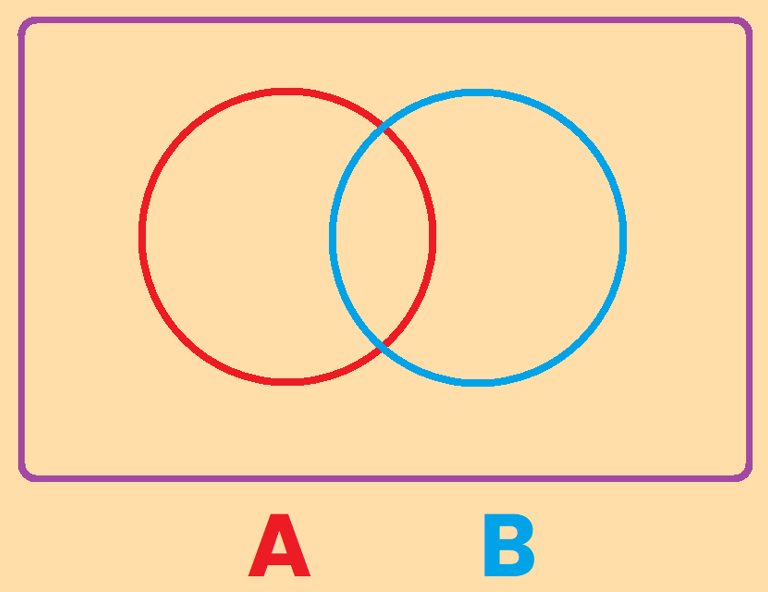
Hay 2 regiones mas que son importantes para este tipo de ejercicios pero para poder definirlas primero tenemos que afrontar EL PROBLEMA DEL HABLA EN ESPAÑA.

En España es corriente utilizar un lenguaje incorrecto a la hora de expresarnos lo que provoca que muchas personas no terminen de comprender este tipo de problemas correctamente, lo voy a ejemplificar.

Un profesor se dirige a sus alumnos y les dice: "Que levanten la mano los que son morenos"

Acto seguido todos los alumnos con el pelo negro levantan la mano.

El profesor aplaude asintiendo y vuelve a decir. "Ok perfecto. Ahora ya pueden bajar la mano." Y pregunta una vez mas "Ahora que levanten la mano los que son rubios"

Acto seguido todos los alumnos con el pelo dorado levantan la mano.

El profesor aplaude nuevamente y dice: "Vale, vale perfecto. Bajad la mano" y pro ultimo preguntó "Ahora que levanten la mano los rubios y los morenos"

Y como todos en el aula tenían o el pelo negro o el pelo dorado levantaron la mano y el profesor empezó a reírse y gritó: "GANÉ!!" . ¿Sabes porque se reía el profesor?

La respuesta es muy fácil: TODOS SE HABÍAN EQUIVOCADO.

Y éste es el famoso problema, y es que no existe nadie tiene el pelo moreno o rubio a la vez. Cuando el profesor preguntó "los rubios Y los morenos" los alumnos entendieron "los rubios O los morenos" porque es costumbre que al hablar en España se use la "Y" cuando realmente queremos decir "O". Es mucho mas fácil entender este fenómeno cuando no son características contrarias como si lo son el ser rubio o moreno.

Cuando por ejemplo miras la característica "ser moreno" y la característica "tener gafas". Si preguntan por los que "tienen gafas Y son morenos" levantarán la mano aquellos que tengan el pelo moreno y al mismo tiempo lleven gafas, sin embargo, si preguntan por "tienen gafas O son morenos" levantarán la mano aquellos que tengan gafas y sean rubios ( porque tienen gafas), levantaran la mano los que no tienen gafas pero son morenos ( porque son morenos) y también levantaran la mano aquellos que son morenos y tienen gafas ( porque cumplen ambos requisitos).

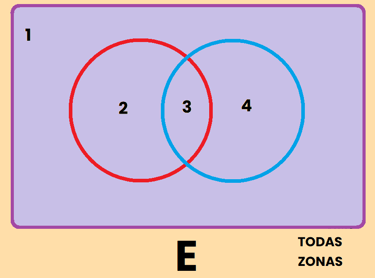
El diagrama vamos a dividirlo en 4 regiones para poder diferenciar claramente a que zona nos referimos en cada momento y que quedan delimitadas por las fronteras de A, B y la región exterior.

• La primera región la llamaremos la zona 1: Y coincide con la región exterior que hemos definido antes (verde)

• La segunda región la llamaremos la zona 2: (rosa)

• La tercer región la llamaremos la zona 3: (naranja)

• La cuarta región la llamaremos la zona 4: (gris)

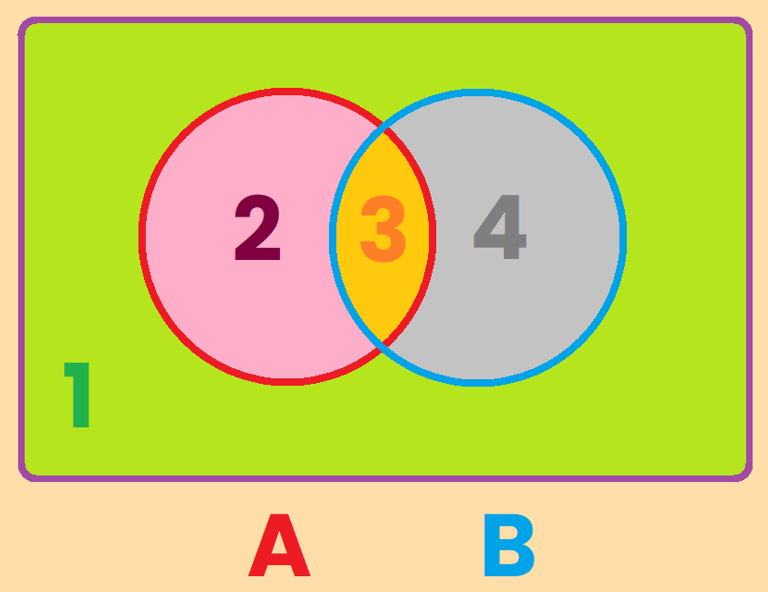
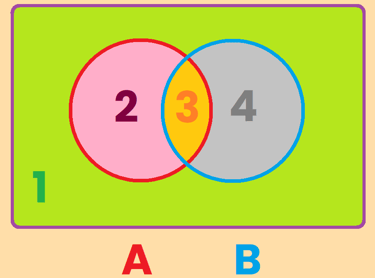
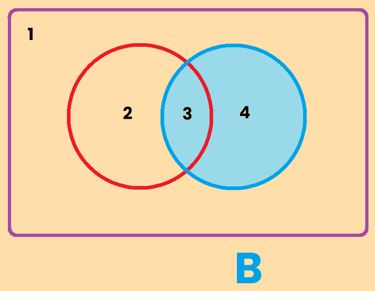
Es importante entonces deducir que el conjunto A esta compuesto por la suma se la zona 2 y la zona 3 y obviamente el conjunto B esta compuesto por la suma se la zona 3 y la zona 4.

OJO!: Es un error muy común definir el conjunto de A como la zona 2 y el conjunto B como la zona 4, sin tener en cuenta la zona 3 que es muy importante y no hay que olvidarse de ella

Así pues se dan estas equivalencias:

• La zona 1 = Región exterior = "Lo que no es ni A ni B"

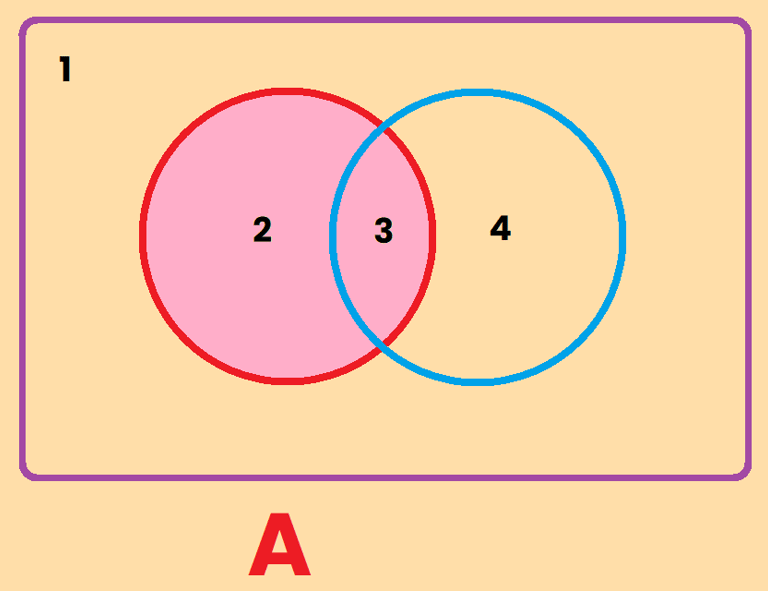
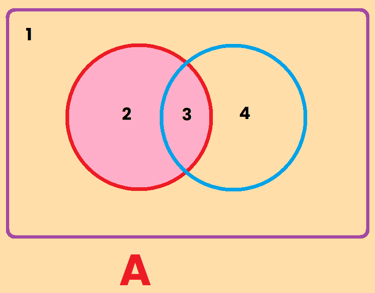
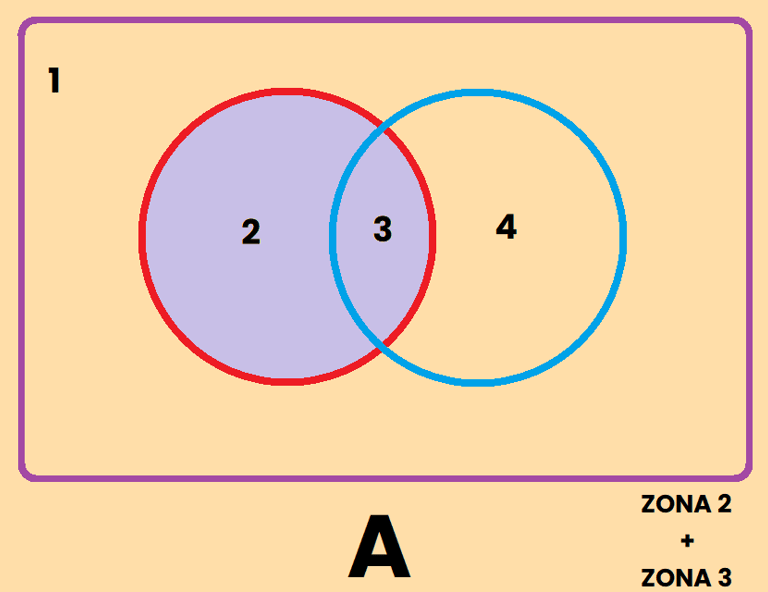
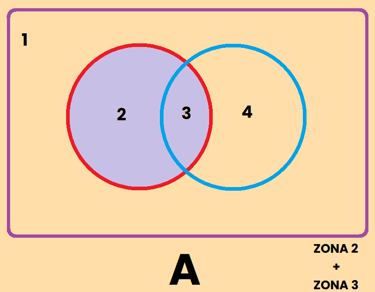
• La zona 2 + 3 = Conjunto de A = "Todo lo que es A"

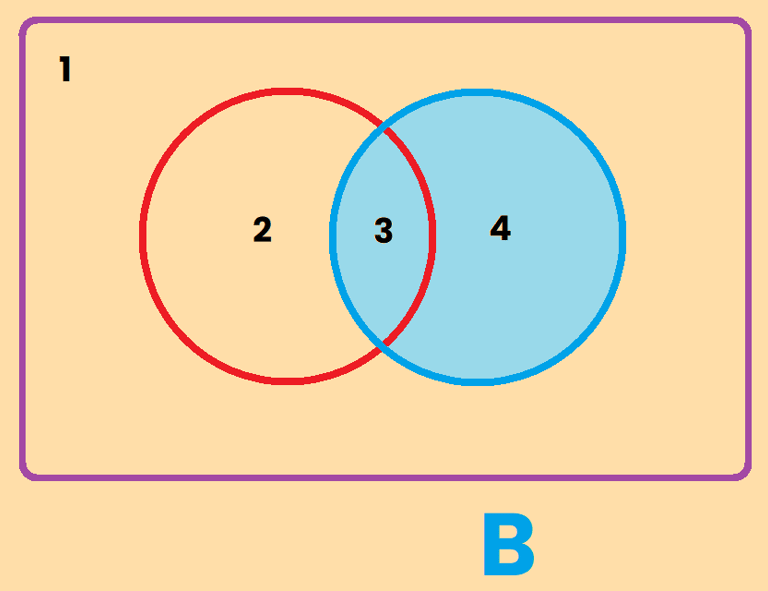
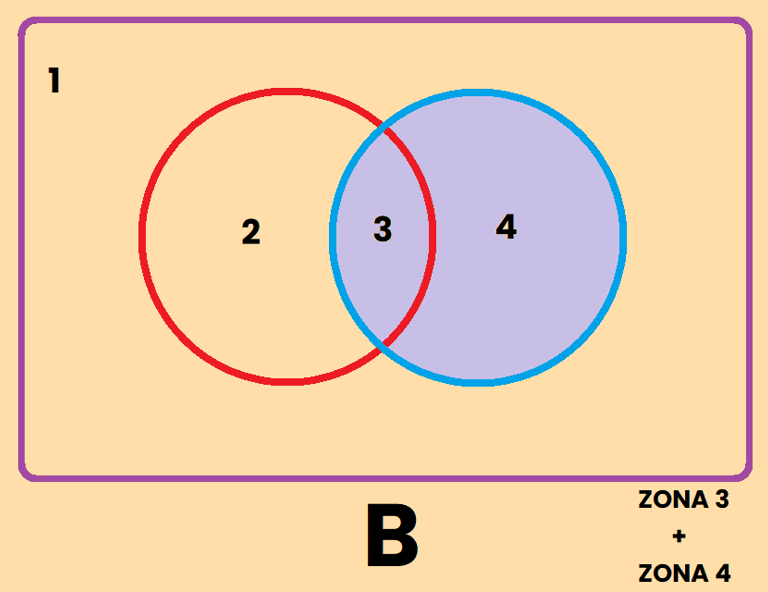
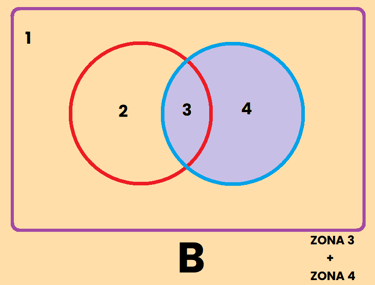
• La zona 3 + 4 = Conjunto de B = "Todo lo que es B"

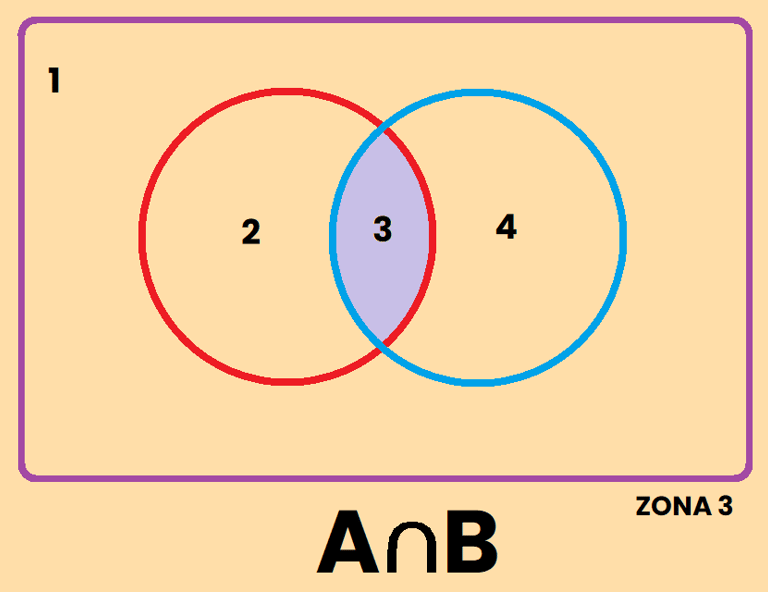
• La zona 3 = "Lo que es A y B al mismo tiempo"

• La zona 2 = "La parte de A que solo es A"

• La zona 4 = "La parte de B que solo es B"

EL PROBLEMA DEL HABLA EN ESPAÑA

Las 2 regiones que nos faltan entonces por definir en este tipo de problema es la unión y la intersección:

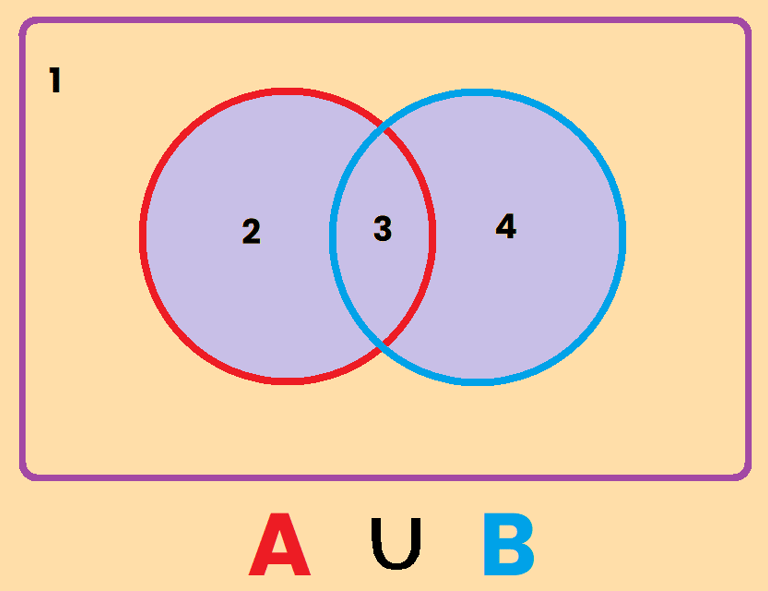
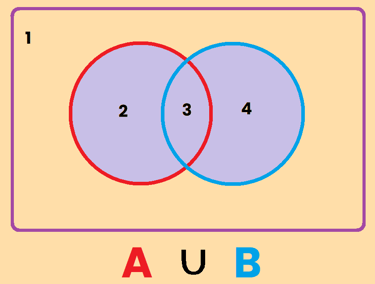
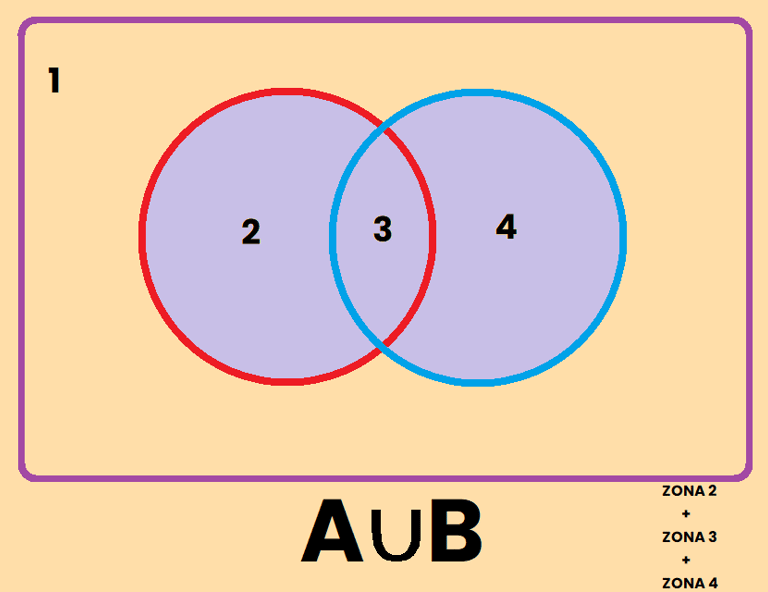
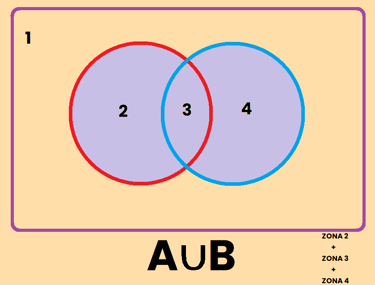
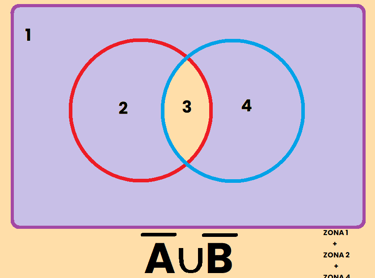
La unión es aquella parte del dibujo que es parte del conjunto A , o del conjunto B o de ambos. Fíjate que en la descripción he usado la letra "o", o bien es una cosa, o la otra o ambas. Por eso la unión representa a aquellos que pertenecen al conjunto de A o al conjunto de B o a ambos, es decir, es la zona 2 + 3 + 4 , y se representa como A∪B

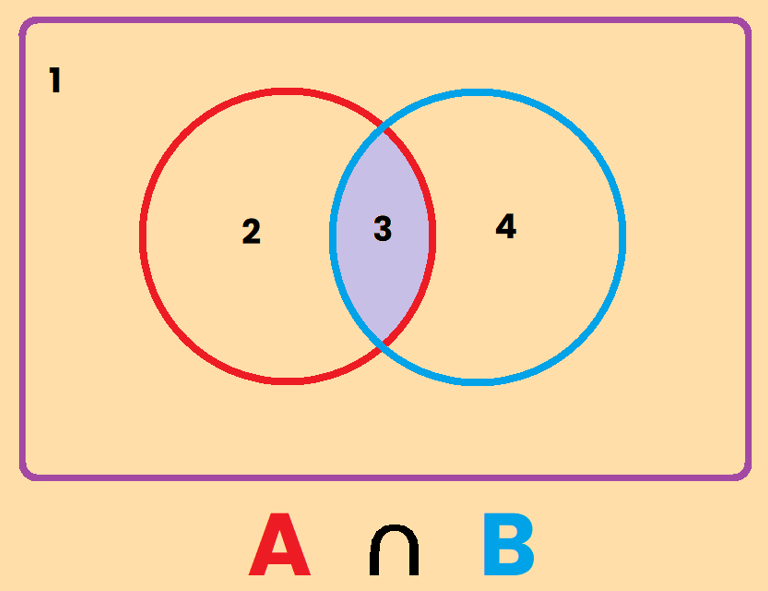
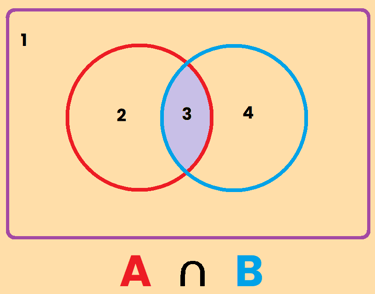
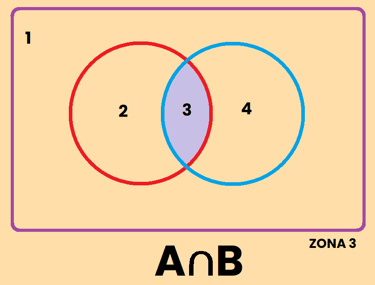
La intersección es aquella parte del dibujo que es parte del conjunto A y del conjunto B al mismo tiempo. Fíjate que en la descripción he usado la letra "y", es A y B. Por eso la intersección representa a aquellos que pertenecen al conjunto de A y al conjunto de B, es decir, es la zona 3 , y se representa como A∩B

CONJUNTOS CONTRARIOS Y CONJUNTO TOTAL

En éste tipo de ejercicios también es común hablar de los contrarios.

Los contrarios representan aquella parte del gráfico que no pertenece al conjunto que hace referencia.

Esto es muy útil porque permite ver o calcular que parte no pertenece al otro o hacer deducciones lógicas al respecto.

Pero para poder calcularlo primero tenemos que entender lo que es el conjunto total. El conjunto total no es mas que la zona 1 + zona 2 + zona 3 + zona 4, es decir, la totalidad del dibujo y por tanto como representa el 100% del dibujo siempre está relacionado con este número o con el 1 si estamos hablando de probabilidades en forma de fracciones

Pongamos un ejemplo: Vamos a suponer que la probabilidad de pertenecer al conjunto A es el 60%. Entonces cual es la probabilidad del contrario?

El contrario supone no pertenecer a A, por lo que seria el 40% pero porqué?. Pues muy fácil, porque si todo es el 100%, y pertenecer a A es el 60%, 100%-60% = 40%.

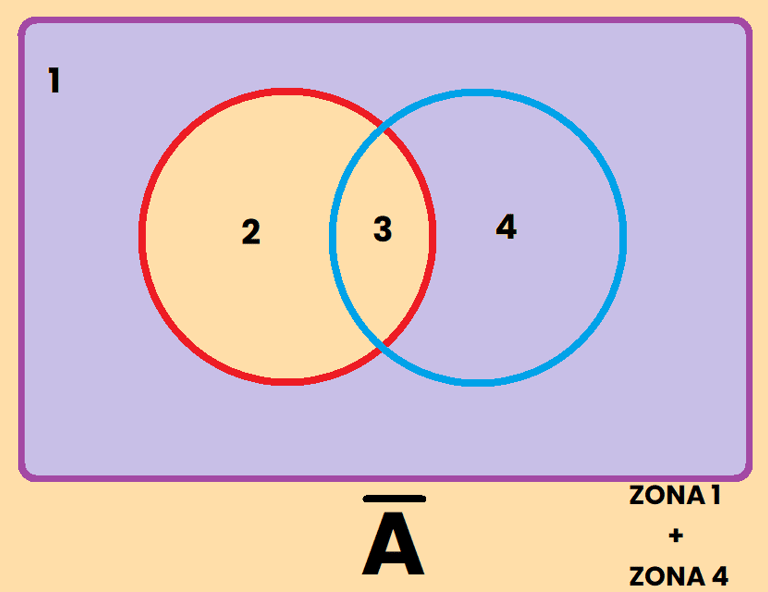
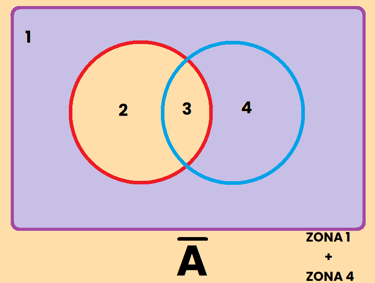
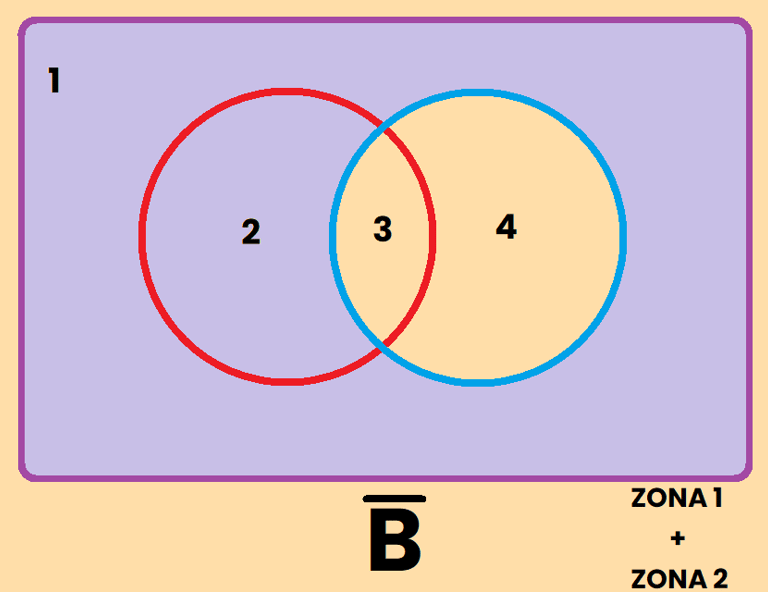
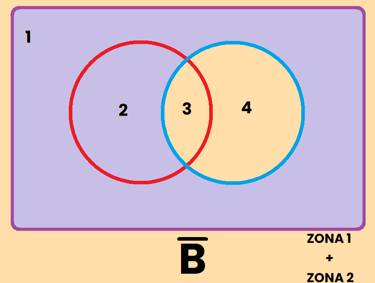
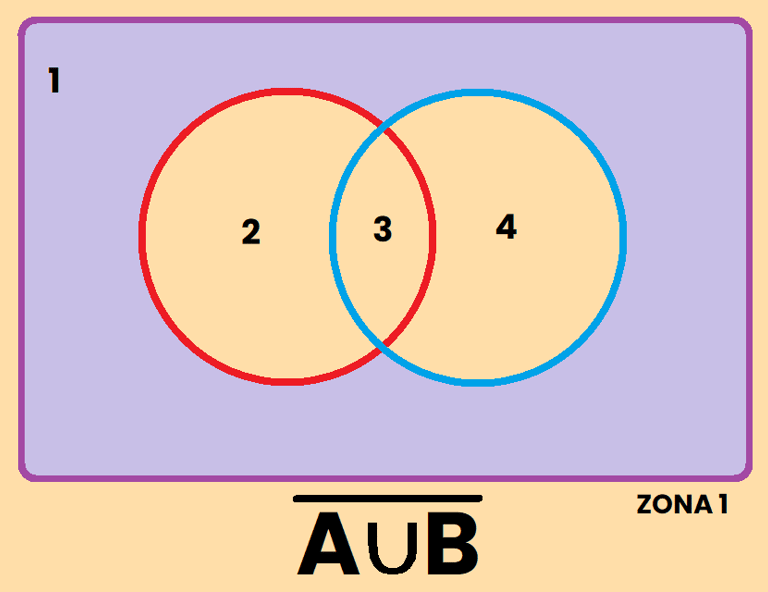
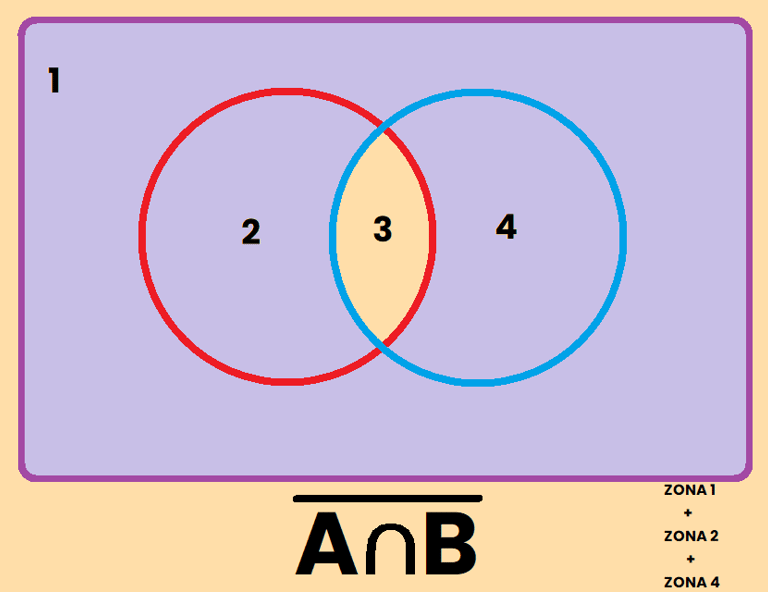
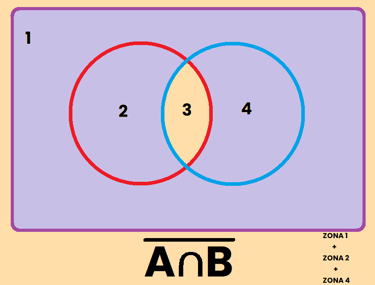
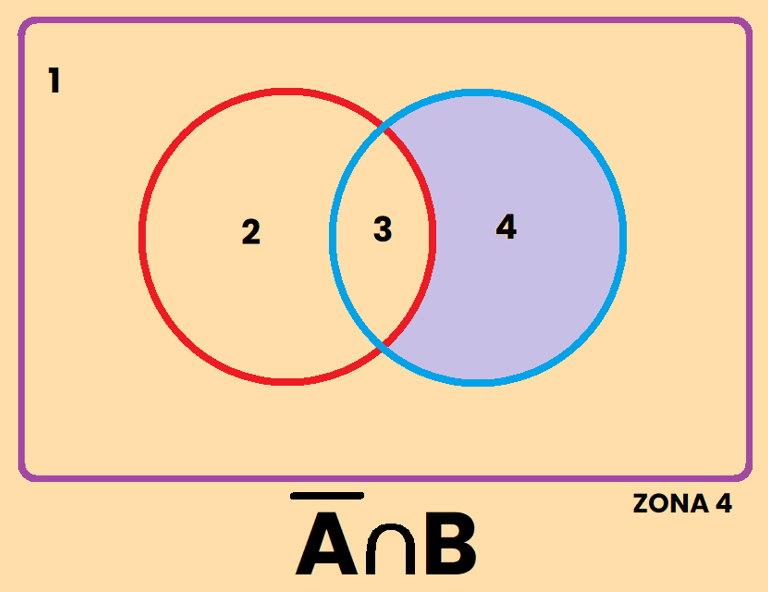
Los contrario se pueden representar de varias formas diferentes, por ejemplo, si tomamos como referencia el conjunto A, el contrario de A se puede representar como:

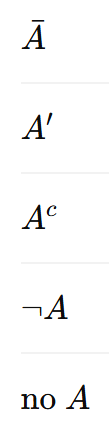
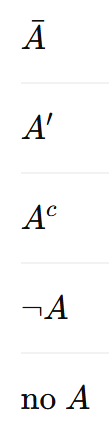
REPRESENTACIÓN DE SUCESOS

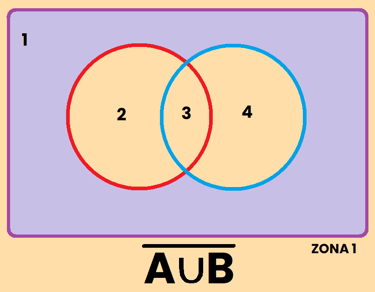
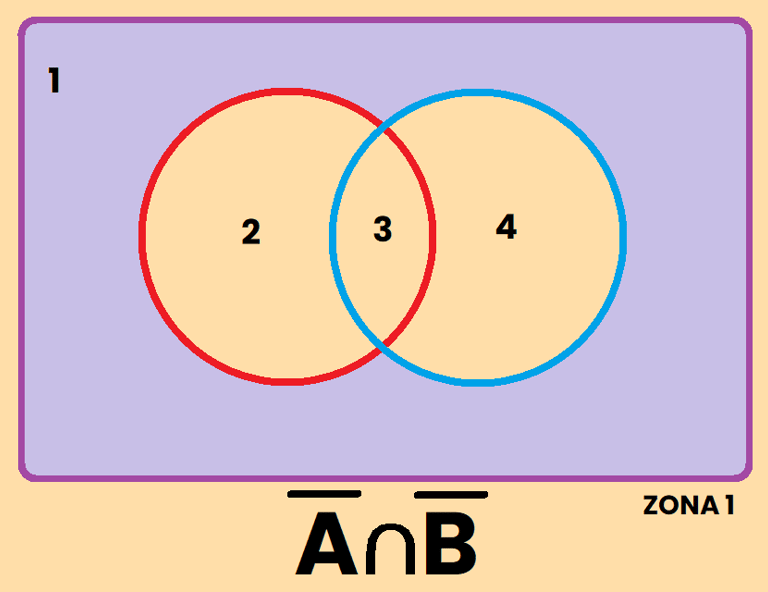
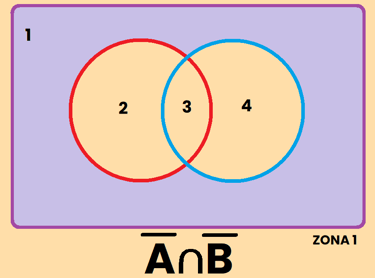
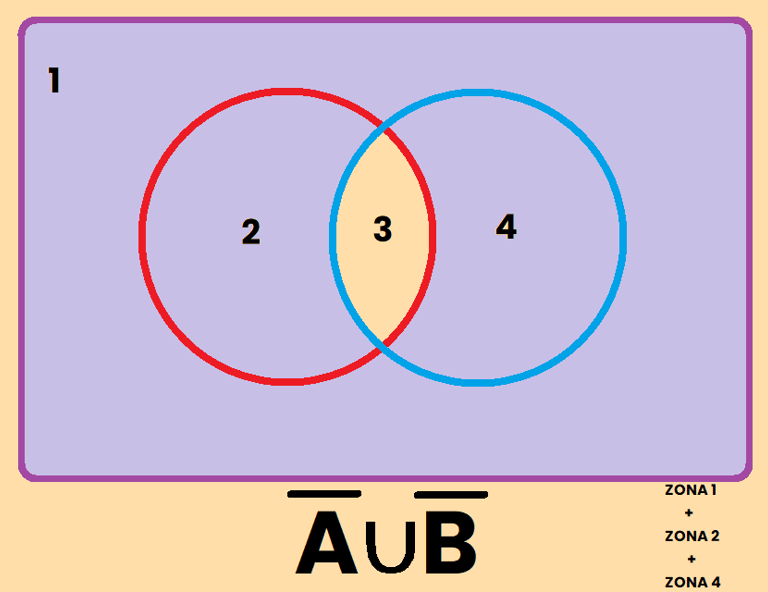
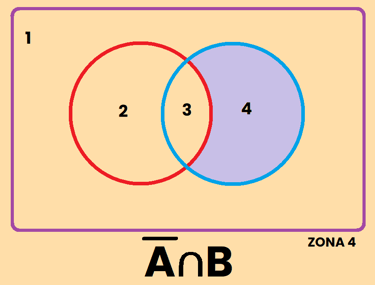
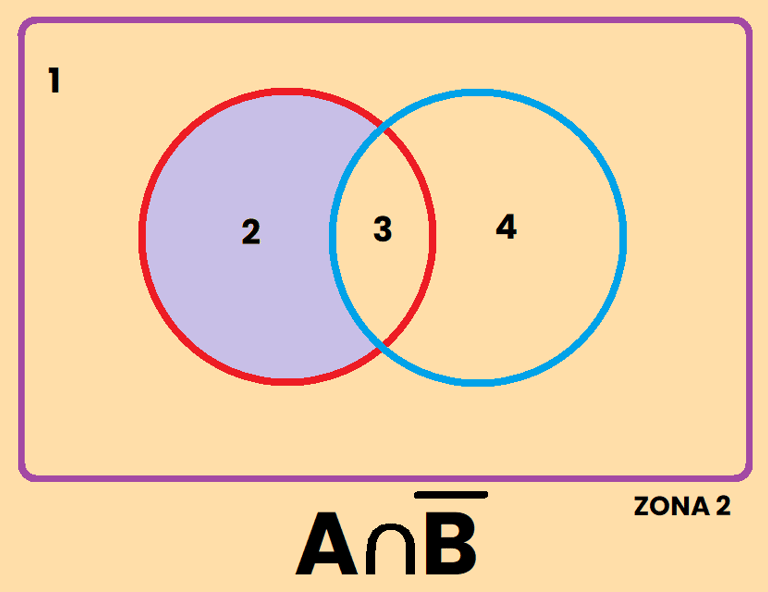
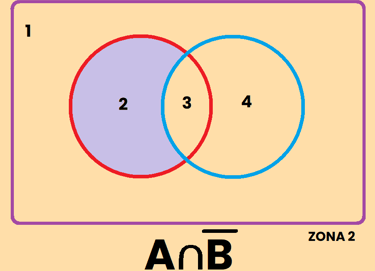
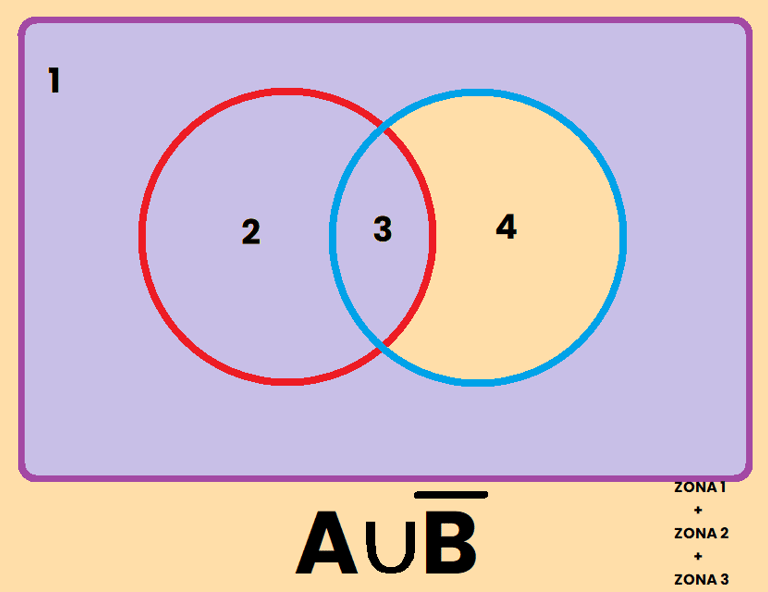
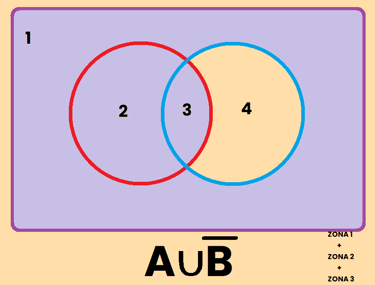
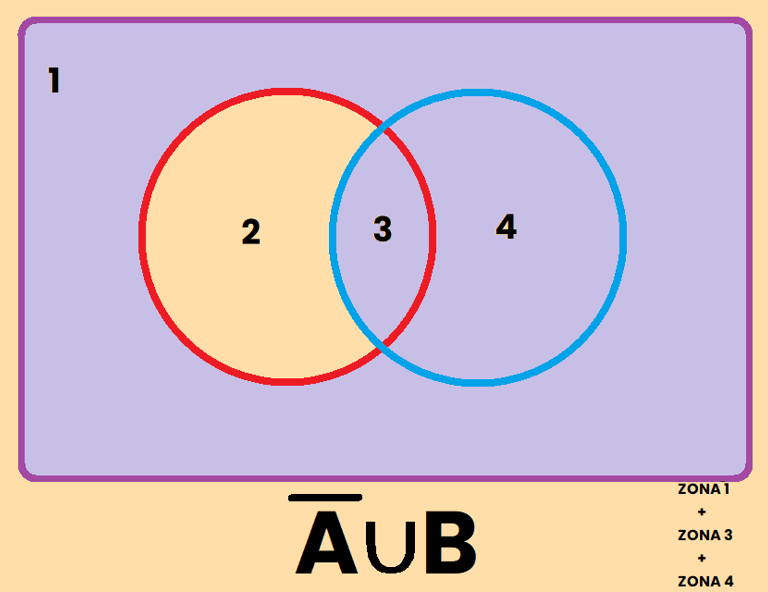
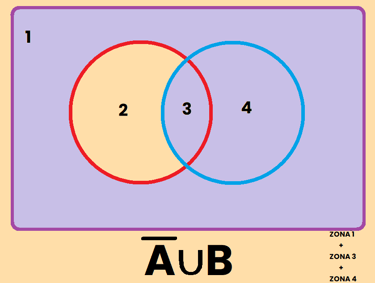
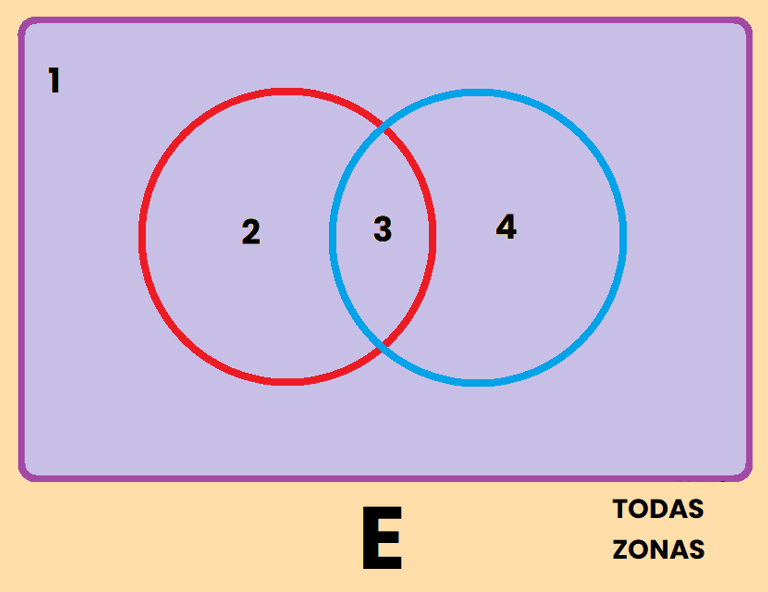
EJEMPLO

Sabiendo que la probabilidad de A es 0,7, ¿cuál es la probabilidad del suceso contrario de A (es decir, de que no ocurra A)?

Pues como A + su contrario siempre suma 1, entonces la probabilidad de que no ocurra A es:
1 – P(A) = 1 – 0,7 = 0,3

Si P(A) = 0,5, P(B) = 0,4 y P(A ∩ B) = 0,2, ¿Cuál es la probabilidad de A ∪ B?

Se aplica la fórmula: como A es zona 2 y 3, B es zona 3 y 4, al sumarlos tenemos 2+3+3+4 zonas, si quitamos la zona 3 que es la zona de la intersección obtendremos la union
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∪ B) = 0,5 + 0,4 – 0,2 = 0,7

Si la probabilidad de A ∪ B es 0,85, P(A) es 0,5 y P(B) es 0,6, ¿Cuál es la probabilidad de A ∩ B?

Reordenamos la fórmula de la unión:
P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
P(A ∩ B) = 0,5 + 0,6 – 0,85 = 0,25

Si P(A) = 0,6 y P(B) = 0,3, siendo A y B incompatibles, ¿Cuál es la probabilidad de A ∪ B?

Si son incompatibles (no pueden suceder a la vez), entonces:
P(A ∩ B) = 0
Así que:
P(A ∪ B) = P(A) + P(B) = 0,6 + 0,3 = 0,9

¿Cuál es la probabilidad de que ocurra A pero no B, si P(A) = 0,7 y P(A ∩ B) = 0,2?

Esto se representa como: P(A ∩ ¬B)
Y se calcula así: Como esta zona es la 2, y A es la zona 2 y 3, si a A le restamos la zona 3, que es la intersección obtendremos la zona 2
P(A ∩ ¬B) = P(A) – P(A ∩ B) = 0,7 – 0,2 = 0,5

Si P(A) = 0,4 y P(B) = 0,5, ¿puede ser P(A ∪ B) = 0,95?

No.
Porque P(A ∪ B) ≤ 1, y como mínimo se solapan en 0,4 + 0,5 – 1 = –0,1, lo que no tiene sentido.
Luego la máxima P(A ∪ B) posible sería 0,9