Programación lineal

Ejemplo resuelto

Un orfebre fabrica dos tipos de joyas. Las del tipo A precisan 1 g de oro y 1,5 g de plata, vendiéndolas a 40 euros cada una. Para la fabricación de las de tipo B emplea 1,5 g de oro y 1 g de plata, y las vende a 50 euros. El orfebre tiene solo en el taller 750 g de cada uno de los metales. Calcula cuántas joyas ha de fabricar de cada clase para obtener un beneficio máximo.

Paso - 1 (IDENTIFICAR LAS VARIABLES)

Las variables son aquellos datos que no conocemos del ejercicio y por el que no están preguntando. En este ejemplo la variables serán:

Variable X= Cantidad de joyas del tipo A

Variable Y = Cantidad de joyas del tipo B

Paso - 2 (RELLENAR LA TABLA)

En la tabla colocaremos las variables y todos aquellos elementos que son característicos de cada una de las joyas y añadimos una ultima columna con el total.

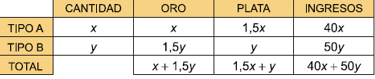
Puesto que la joya del Tipo A la cantidad es "X", y el oro que necesita dicha joya es 1G, el total de oro empleado en la fabricación de todas las joyas del tipo A será "x*1 = x", por eso en la casilla del oro hay una x. Del mismo modo la cantidad de plata usada en las joyas del tipo A es 1,5 gramos. Como la cantidad de joyas del Tipo A no lo sabemos "X", la cantidad de plata utilizada para hacer joyas del tipo A será "x*1.5=1.5X". Y de la misma manera como los ingresos por cada joya A es, 40€, el total de ingresos por las joyas del tipo A será "40*x=40x".

Hacemos este mismo proceso para la joya del Tipo B

Y en la última columna colocamos los totales. Si el total de oro usado en la joyas del tipo A es X, y la cantidad total de oro en las joyas del Tipo B es 1.5Y, es lógico pensar que el total de oro utilizado en ambas joyas es "x+1.5Y". Lo mismo ocurre con el resto de columnas

Paso - 3 (RESTRICCIONES)

Las restricciones no es mas que plantear las inecuaciones del problema. (la inecuaciones no es mas que plantear las ecuaciones pero utilizando los símbolos de ">","≥","<" o "≤".

En éste ejemplo cómo x+1.5y representa el total de oro utilizado para producir ambas joyas, y el enunciado dice "el orfebre tiene 750g de cada uno de los metales", es lógico pensar que el total de oro que se puede gastar en fabricar las joyas es 750 o menos, pero nunca mas porque es físicamente imposible gastar mas oro que el que hay por eso

"x+1.5y ≤ 750 " Esta restricción lo que nos dice es que el total de oro usado en las joyas "x+1.5y" tiene que ser menor o igual al oro del almacén que poseemos "750".

Y lógicamente la otra restricción será:

"1.5x+y ≤ 750 " Esta restricción lo que nos dice es que el total de plata usada en las joyas "1.5x+y" tiene que ser menor o igual a la plata del almacén que poseemos "750".

Paso - 4 (RESTRICCIONES OCULTAS)

Las restricciones ocultas son restricciones que se "sobreentienden" del planteamiento del ejercicio. No es mas que plantear las inecuaciones del problema. (la inecuaciones no es mas que plantear las ecuaciones pero utilizando los símbolos de ">","≥","<" o "≤".

En éste ejemplo solo tiene sentido de hablar de cantidades positivas tanto de las joyas del Tipo A como del las joyas del Tipo B, puesto que no se pueden fabricar cantidades negativas.

Las restricciones ocultas son:

x ≥ 0

Y ≥ 0

Paso - 5 (FUNCIÓN OBJETIVO)

Es aquella ecuación que hay dentro de la tabla que no tiene una restricción, sino que lo que se pretende es maximizar o minimizarla.

En este caso seria la ecuación de los ingresos:

"40x+50y= z" Z es una variable que se añade para poder demostrar que es la función objetivo

Paso - 6 (TABLA DE VALORES)

Una vez llegado a este punto transformamos las inecuaciones, en ecuaciones y recomiendo que utilicéis colores para diferenciar las ecuaciones e intentar resolver los valores para x=0 e y=0

Vamos a definir colores las ecuaciones y calculamos el valor de x=0 e y=0

x+1.5y≤750 la transformamos en ecuación

x+1.5y=750 y calculamos el valor de x=0 e y=0

x=0; substituimos en la ecuación, 0+1.5y=750 , y= (750/1.5)=500

y=0; substituimos en la ecuación, x+1.5·0=750 , x= 750

1.5x+y≤750 la transformamos en ecuación

1.5x+y=750 y calculamos el valor de x=0 e y=0

x=0; substituimos en la ecuación, 1.5·0+y=750 , y=750

y=0; substituimos en la ecuación, 1.5x+0=750 , x= (750/1.5)=500

Las restricciones de x ≥ 0 e y ≥ 0 no necesita datos en la tabla de valores porque son una línea vertical y otra horizontal, pero si se le asigna color para luego saber reconocerlas

Paso - 7 (REPRESENTAR)

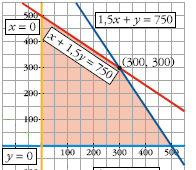
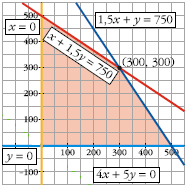
Paso - 8 (VALIDAR ÁREA)

Validar consiste en tomar un valor y preguntarle a la inecuación si se cumple dicha regla para saber que parte de la recta es solución y que parte no lo es. Mi recomendación es siempre escoger un punto en el que la "X" y la "Y" valgan lo mismo , que no estén en ninguna la las rectas que acabamos de representar y que se pueda apreciar claramente que no es parte de ninguna de las rectas.

En este ejemplo por ejemplo escogemos el (100,100)

La preguntamos a la inecuación roja: x+1.5y≤750 para el valor (100,100) sustituyendo los valoras y comprobando si se cumple

¿ 100+1.5·100≤750 ?

¿ 100+150≤750 ?

¿ 250≤750 ? Como 250 si que es menor o igual que 750, si que se cumple la inecuación por lo que el (100,100) si que es parte de la solución para esta inecuación. Por lo que dibujamos 2 flechas sobre la recta indicando la región que si que es solución y continuamos

La preguntamos a la inecuación azul: 1.5x+y≤750 para el valor (100,100) sustituyendo los valoras y comprobando si se cumple

¿ 1.5·100+100≤750 ?

¿ 150+100≤750 ?

¿ 250≤750 ? Como 250 si que es menor o igual que 750, si que se cumple la inecuación por lo que el (100,100) si que es parte de la solución para esta inecuación. Por lo que dibujamos 2 flechas sobre la recta indicando la región que si que es solución y continuamos

La preguntamos a la inecuación naranja: x ≥ 0 para el valor (100,100) sustituyendo los valoras y comprobando si se cumple

¿ 100 ≥ 0 ? Como 100 si que es mayor o igual que 0, si que se cumple la inecuación por lo que el (100,100) si que es parte de la solución para esta inecuación. Por lo que dibujamos 2 flechas sobre la recta indicando la región que si que es solución y continuamos

La preguntamos a la inecuación naranja: y ≥ 0 para el valor (100,100) sustituyendo los valoras y comprobando si se cumple

¿ 100 ≥ 0 ? Como 100 si que es mayor o igual que 0, si que se cumple la inecuación por lo que el (100,100) si que es parte de la solución para esta inecuación. Por lo que dibujamos 2 flechas sobre la recta indicando la región que si que es solución.

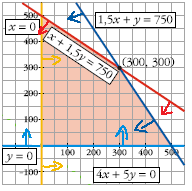
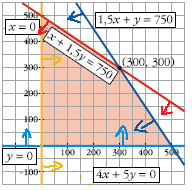
La solución será aquella región que cumplen todas las restricciones, es decir, aquella región a la que apunten todas las fechas. Es región se denomina la región factible .

Paso - 9 (VÉRTICES)

Una vez definida la región factible hay que calcular todos los vértices de la región factible ya que la solución del problema se haya en uno de ellos.

Para ello podemos usar los puntos de intersección que conozcamos del punto 6 de esta explicación o bien en el caso de no conocerlo hay que calcularlo resolviendo el sistema de ecuaciones de las 2 rectas

En este caso hay 3 puntos que ya conocemos

El cruce de la recta naranja con la celeste es el vértice A (0,0)

El cruce de la recta azul con la celeste es el vértice B (500,0)

El cruce de la recta naranja con la roja es el vértice C (0,500)

El cruce de la recta azul y roja es el que quedaría por calcular que es el vértice D

x+1.5y=750

1.5x+y=750

La solución de estas 2 ecuaciones es el punto (300,300) si quieres saber como resolver sistemas de ecuaciones consulta nuestro apartado

Paso - 10 (VALIDAR LA FUNCION OBJETIVO)

Por último, recuperamos la función objetivo que habíamos establecido en el punto 5, y la validamos par los distintos vértices

El cruce de la recta naranja con la celeste es el vértice A (0,0)

40x+50y= z; 40·0+50·0=0+0=0€

El cruce de la recta azul con la celeste es el vértice B (500,0)

40x+50y= z; 40·500+50·0=20000+0=20000€

El cruce de la recta naranja con la roja es el vértice C (0,500)

40x+50y= z; 40·0+50·500=0+25000=25000€

El cruce de la recta azul con la roja es el vértice D (300,300)

40x+50y= z; 40·300+50·300=12000+15000=27000€

Como el valor que estamos buscando es el máximo este se alcanza en el vértice D con la producción de 300 joyas del Tipo A y 300 joyas del Tipo B