La Probabilidad Total

¿En qué consiste la Regla de la probabilidad total?

Ejemplo práctico Probabilidad total

En pruebas sucesivas también funciona la probabilidad total

Enrique Requena

Ceo Classnova y profesor de Matemáticas aplicadas

Conclusión de la Probabilidad Total

La Probabilidad Total es una herramienta poderosa para resolver problemas complejos descomponiéndolos en partes más simples. Permite calcular probabilidades cuando los escenarios están bien definidos, tanto en experimentos únicos como en procesos sucesivos.

En Classnova enseñamos a los estudiantes a manejar esta regla con ejemplos claros y diagramas de árbol que facilitan la comprensión..

En probabilidad muchas veces no conocemos directamente la probabilidad de un suceso, pero sí sabemos cómo se reparte en distintos casos o escenarios. La Regla de la Probabilidad Total nos permite calcularla utilizando esa información.

Si un experimento se puede dividir en varios sucesos incompatibles, A1, A2, A3, ... , An que cubren todo el espacio muestral, entonces la probabilidad de un suceso S se puede calcular así:

Imagina que queremos calcular la probabilidad de que un teléfono esté averiado en un país. Este dato no lo conocemos y es difícil de saber con exactitud que probabilidad es.

Lo que si que sabemos es que en el país solo se venden 3 marcas de móviles

• Punkia

• Pijia

• Kakia

Aunque no sabemos la probabilidad de que el teléfono este averiado en el país, si que sabemos que las 3 únicas marcas que operan en el país son las 3 mencionadas anteriormente, es decir, las 3 cubren la totalidad del espacio muestral de teléfonos que hay en el país.

Además las marcas si que conocen sus propios datos, y si que saben la probabilidad de que uno de sus teléfonos esté averiados. Es lógico, pues, deducir que la probabilidad de que un móvil esté averiado en el país es igual a la probabilidad de que un móvil esté estropeado de cada una de las marcas multiplicado por el peso que tiene la marca en el mercado

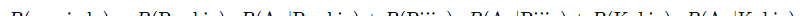
La regla de la probabilidad total también se aplica cuando un suceso puede alcanzarse a través de varias rutas.

Por ejemplo, en un diagrama en árbol de dos etapas:

• Primero ocurre uno de los sucesos A1, A2, A3,..., An

• Luego dentro de cada caso puede cumplirse o no el suceso (S)

Continuando con el ejemplo anterior y utilizando los siguientes datos:

• La cuota de mercado de Punkia es 3/6

• La cuota de mercado de Pijia es 2/6

• La cuota de mercado de Kakia es 1/6

• La probabilidad de que un móvil de Punkia esté averiado es 1/10

• La probabilidad de que un móvil de Pijia esté averiado es 1/4

• La probabilidad de que un móvil de Kakia esté averiado es 1/2

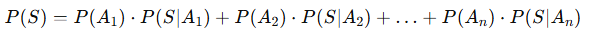
En otras palabras, descomponemos el suceso S, en partes mas pequeñas, pero que la totalidad de las partes, componen todo el espacio muestral

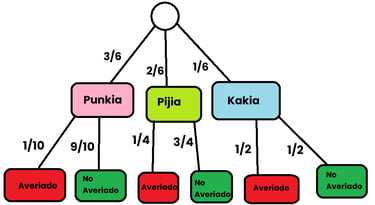
El diagrama de árbol queda de la siguiente manera. Primeramente hay 3 sucesos diferentes y es que el móvil pueda ser de una de las 3 marcas, y tal y como ya hemos comentado anteriormente las 3 llenan la totalidad del espacio muestral porque 3/6 + 2/6 + 1/6 =1

Y posteriormente el móvil puede estar averiado o no, las probabilidades de que un móvil esté averiado las da el enunciado, y la probabilidad que no lo esté se calcula fácilmente con la fórmula del complementario.

Así pues de cada una de las ramas solo nos interesará la parte averiada y como estamos sumando la probabilidad de móviles averiados de cada marca multiplicándolo por su cuota de mercado y no existe ningún otro móvil averiado que no sea alguno de esto tres, la probabilidad de que un móvil en el país esté averiado es la suma de que esté averiado en cada una de las marcas por la probabilidad de que el móvil sea de esa marca

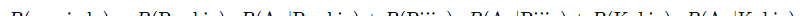
P(Averiado)=(3/6) * (1/10) + (2/6) * (1/4) + (1/6) * (1/2)