¿Qué dicen las Leyes de De Morgan?
Ejemplo primera ley de Morgan: notas en un examen
Ejemplo segunda ley de Morgan: lanzar un dado


Importancia de estas leyes


Enrique Requena
Ceo Classnova y profesor de Matemáticas aplicadas
Conclusión Leyes de Morgan
Comprender y aplicar las Leyes de De Morgan es esencial en el estudio de la probabilidad. Gracias a ellas, los problemas se vuelven más manejables y las expresiones mucho más claras.
En Classnova enseñamos a nuestros estudiantes a utilizarlas con ejemplos prácticos y situaciones cotidianas, facilitando su comprensión paso a paso.
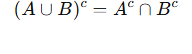
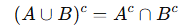
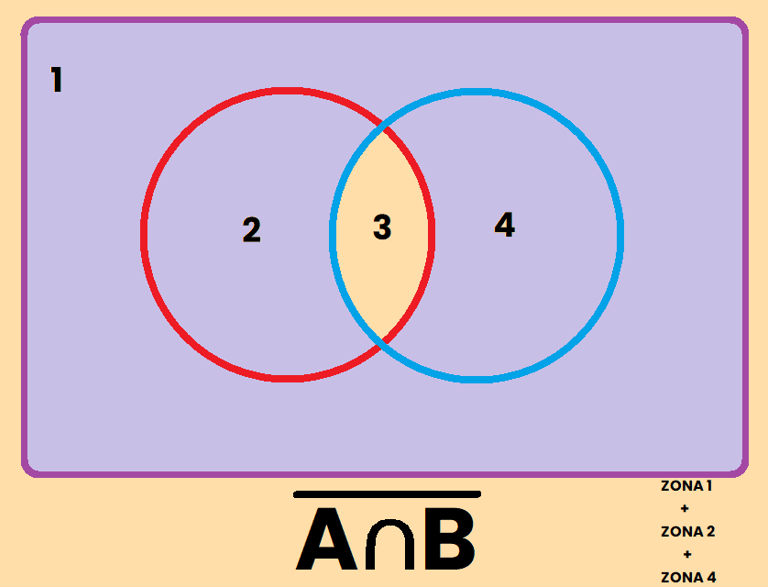
Existen dos leyes principales:
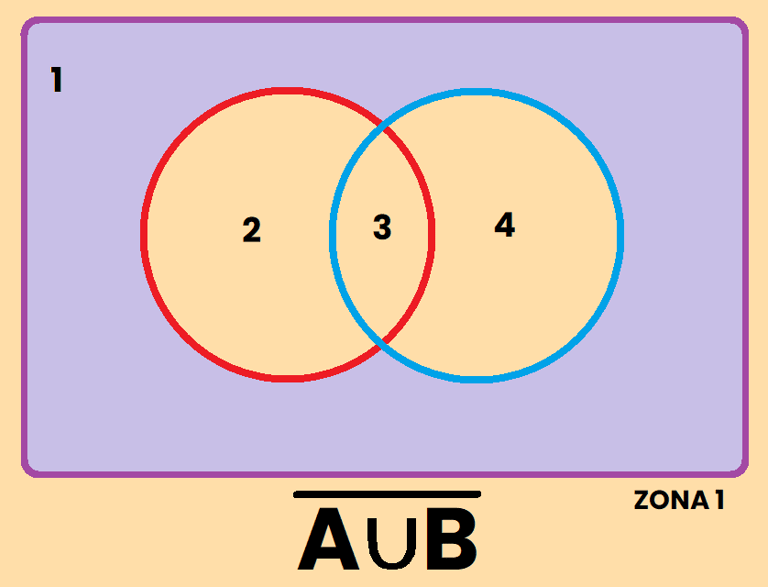
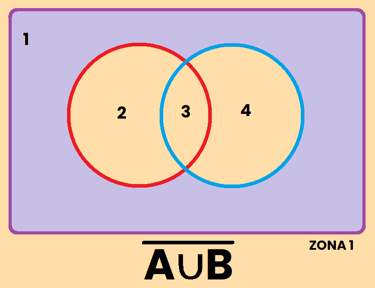
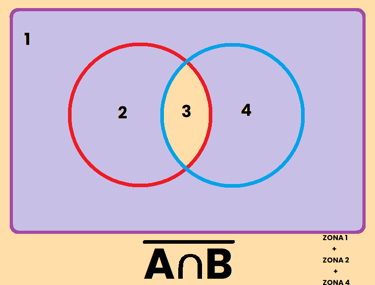
1) El complemento de la unión es igual a la intersección de los complementos:
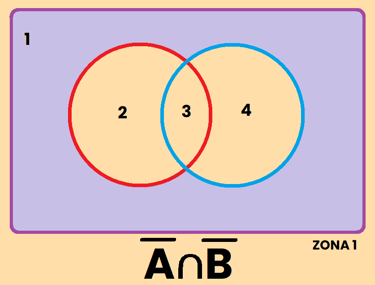
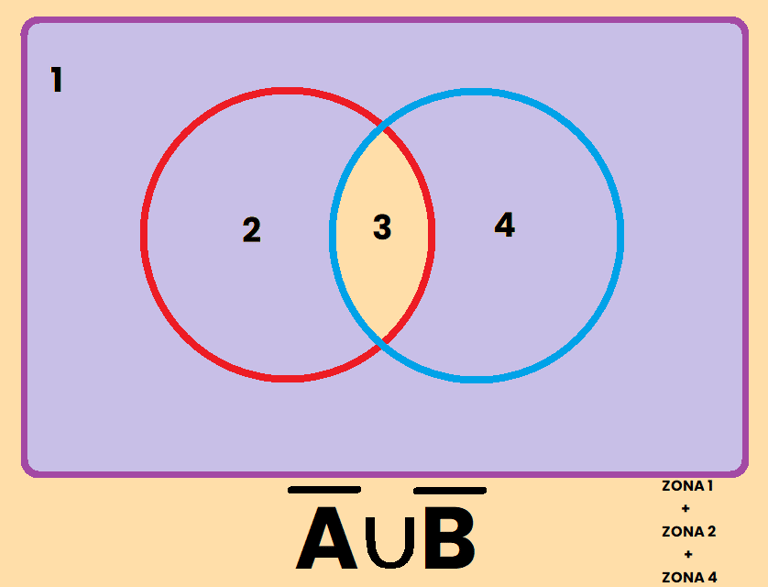
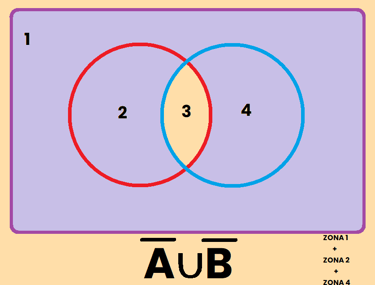
2) El complemento de la intersección es igual a la unión de los complementos:
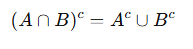
Comprobamos ambas regiones
Sea A = “aprobar matemáticas”
Sea B = “aprobar lengua”
La primera ley nos dice que “no aprobar ni matemáticas ni lengua” es equivalente a “suspender matemáticas y suspender lengua al mismo tiempo”.
A = “sacar un número par” {2, 4, 6}
B = “sacar un número mayor que 3” {4, 5, 6}
La segunda ley nos indica que el contrario de “sacar un número par y mayor que 3” equivale a “sacar un número que no sea par o que no sea mayor que 3”.
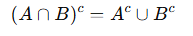
Las Leyes de De Morgan permiten:
Simplificar cálculos con sucesos y probabilidades.
Transformar expresiones complejas en equivalencias más fáciles de manejar.
Relacionar operaciones con sucesos (unión, intersección y complementos).
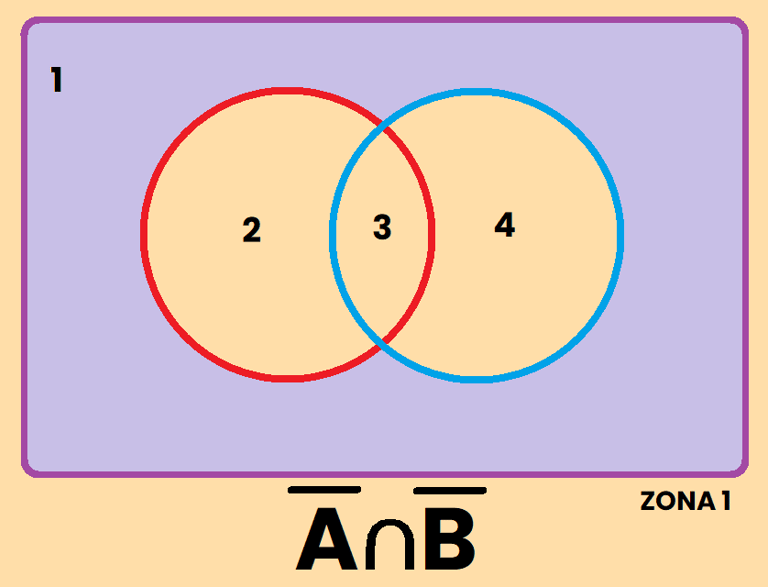
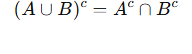
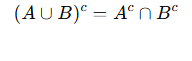
Las Leyes de De Morgan en probabilidad
Cuando trabajamos con sucesos en probabilidad, el uso de los complementos puede parecer complejo al principio. Sin embargo, las Leyes de De Morgan nos ayudan a simplificar expresiones y a razonar de forma ordenada. Estas leyes son fundamentales tanto en matemáticas como en lógica y probabilidad.
MATEMÁTICAS CCSSBACHILLERATOPROBABILIDADMATEMÁTICASEXPLICACIÓN
Enrique
9/16/20252 min leer
