Propiedades distributiva numero 1
Las operaciones entre sucesos cumplen la misma lógica que en el álgebra:
Primera propiedad distributiva: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Propiedades distributiva numero 2
Las operaciones entre sucesos cumplen la misma lógica que en el álgebra:
Segunda propiedad distributiva: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Propiedades de simplificación 1

Propiedades de simplificación 2


Enrique Requena
Ceo Classnova y profesor de Matemáticas aplicadas
Propiedades del complemento
El complemento de un complemento devuelve el suceso original:
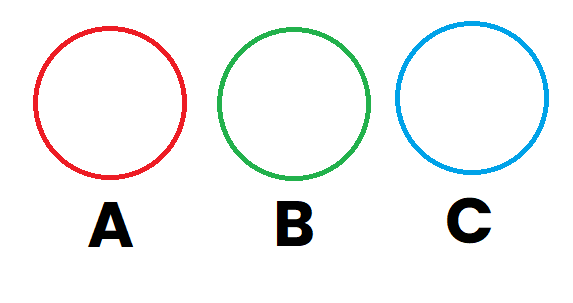
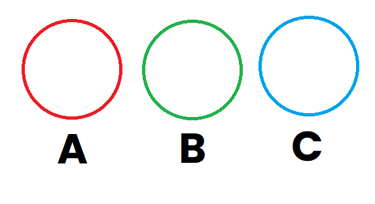
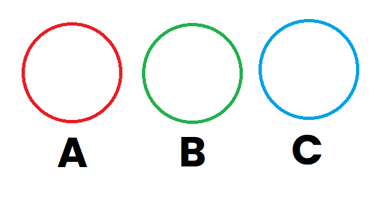
Imaginemos que tenemos 3 sucesos, A , B y C representados por el color Rojo, Verde y Azul respectivamente
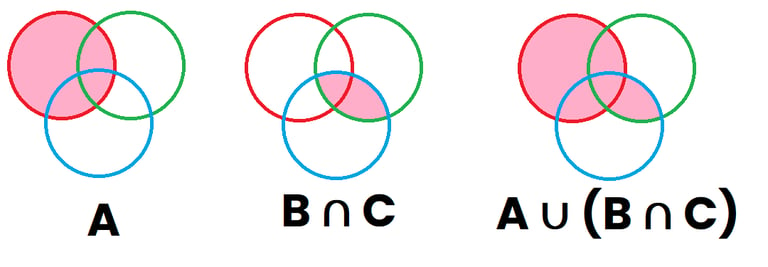
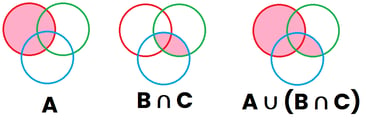
Suponiendo que dichos sucesos tienen elementos compartidos entre ambos sucesos, los 3 sucesos quedan superpuestos unos encima de otros. Ahora vamos a marcar de color Rosa en el primer dibujo lo que representa el suceso "A" (primer dibujo), Posteriormente vamos a pintar de rosa lo que representa "B∩C" que es la región que es verde y azul al mismo tiempo (segundo dibujo), y por último vamos a representar "A∪(B∩C)", que son aquellas regiones que o bien están pintadas en el dibujo 1 o bien están pintadas en el dibujo 2 y da como resultado (tercer dibujo)
Ahora vamos a representar la región "A∪B" (primer dibujo), Posteriormente vamos a pintar de rosa lo que representa "A∪C" (segundo dibujo), y por último vamos a representar "(A∪B)∩(A∪C)", que son todas aquellas zonas que están pintadas en el dibujo 1 y en el dibujo 2, y dan como resultado (tercer dibujo)
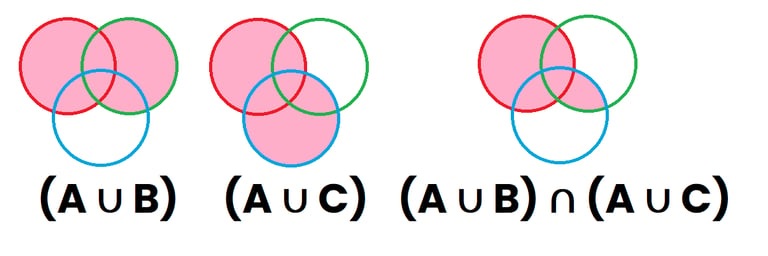
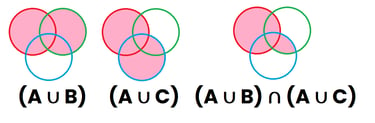
Como se puede comprobar, el tercer dibujo de ambas representaciones representan el mismo área, quedando demostrado que : A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Imaginemos que tenemos 3 sucesos, A , B y C representados por el color Rojo, Verde y Azul respectivamente
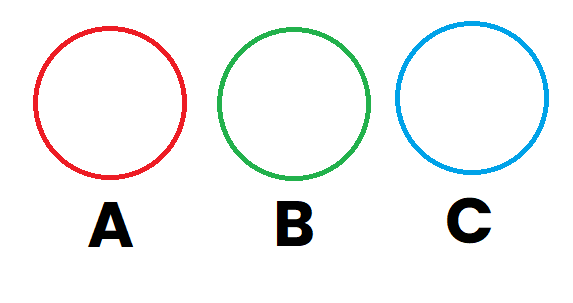
Suponiendo que dichos sucesos tienen elementos compartidos entre ambos sucesos, los 3 sucesos quedan superpuestos unos encima de otros. Ahora vamos a marcar de color Rosa en el primer dibujo lo que representa el suceso "A" (primer dibujo), Posteriormente vamos a pintar de rosa lo que representa "B∪C" que es la región que es verde o azul (segundo dibujo), y por último vamos a representar "A∩(B∪C)", que son aquellas regiones que están pintadas en el dibujo 1 y también están pintadas en el dibujo 2 y da como resultado (tercer dibujo)
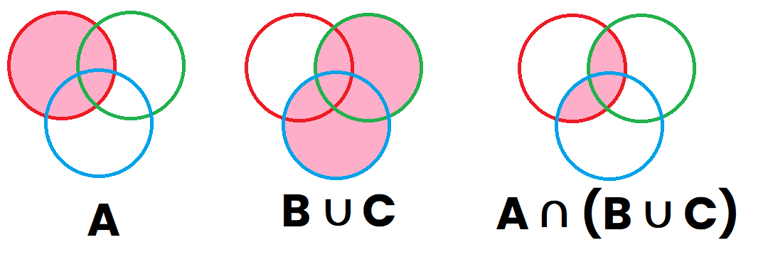
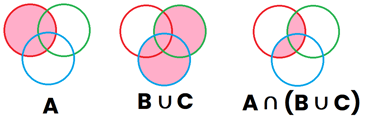
Ahora vamos a representar la región "A∪B" (primer dibujo), Posteriormente vamos a pintar de rosa lo que representa "A∪C" (segundo dibujo), y por último vamos a representar "(A∪B)∩(A∪C)", que son todas aquellas zonas que están pintadas en el dibujo 1 y en el dibujo 2, y dan como resultado (tercer dibujo)
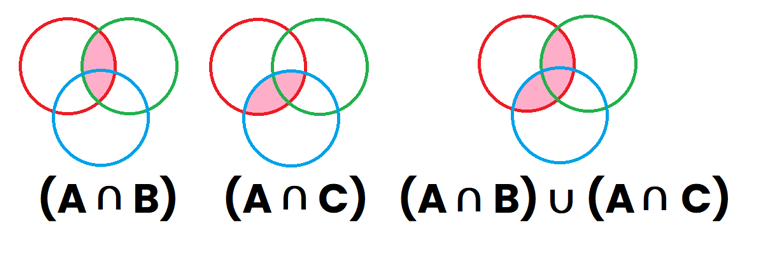
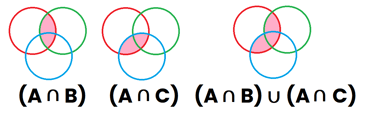
Como se puede comprobar, el tercer dibujo de ambas representaciones representan el mismo área, quedando demostrado que : A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A veces, combinar un suceso con él mismo dentro de una operación no cambia el resultado:
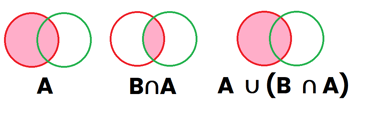
Primera propiedad de simplificación: A ∪ (B ∩ A) = A
Imaginemos que tenemos 2 sucesos, A y B representados por el color Rojo y Verde respectivamente
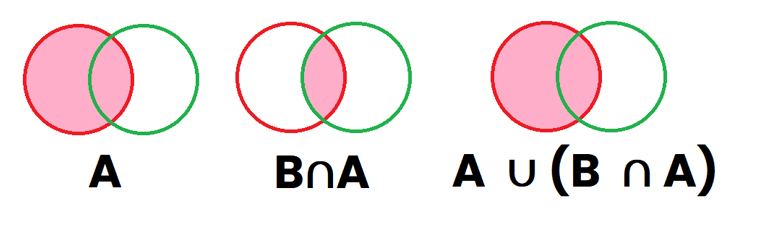
Suponiendo que dichos sucesos tienen elementos compartidos entre ambos sucesos, los 2 sucesos quedan superpuestos uno encima del otro. Ahora vamos a marcar de color Rosa en el primer dibujo lo que representa el suceso "A" (primer dibujo), posteriormente vamos a pintar de rosa lo que representa "B∩A" que es la región que es roja y verde al mismo tiempo (segundo dibujo), y por último vamos a representar "A∪(B∩A)", que son aquellas regiones que están pintadas en el dibujo 1 o en el dibujo 2 (tercer dibujo), por lo que se ve a simple vista que el dibujo 1 y 3 son iguales, por lo que A ∪ (B ∩ A) = A
A veces, combinar un suceso con él mismo dentro de una operación no cambia el resultado:
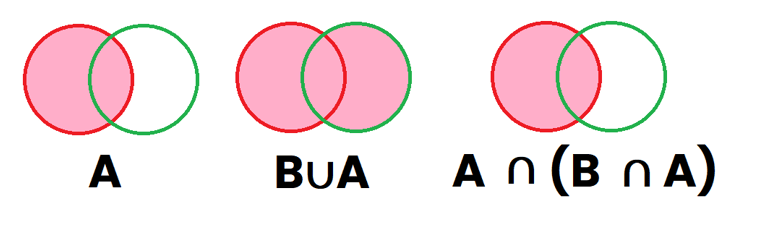
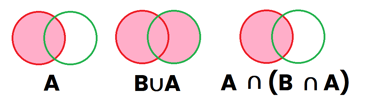
Segunda propiedad de simplificación: A ∩ (B ∪ A ) = A
Imaginemos que tenemos 2 sucesos, A y B representados por el color Rojo y Verde respectivamente


Suponiendo que dichos sucesos tienen elementos compartidos entre ambos sucesos, los 2 sucesos quedan superpuestos uno encima del otro. Ahora vamos a marcar de color Rosa en el primer dibujo lo que representa el suceso "A" (primer dibujo), posteriormente vamos a pintar de rosa lo que representa "B∪A" que es la región que es roja o que es verde (segundo dibujo), y por último vamos a representar "A∩(B∪A)", que son aquellas regiones que están pintadas en el dibujo 1 y también en el dibujo 2 (tercer dibujo), por lo que se ve a simple vista que el dibujo 1 y 3 son iguales, por lo que A ∩ (B ∪ A ) = A
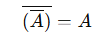
Propiedades de las operaciones con sucesos
En probabilidad, los sucesos se pueden combinar mediante operaciones como la unión, la intersección o el complemento. Estas operaciones cumplen una serie de propiedades que nos permiten simplificar y trabajar con expresiones de manera más sencilla.
MATEMÁTICAS CCSSBACHILLERATOPROBABILIDADMATEMÁTICASEXPLICACIÓN
Enrique
9/12/20254 min leer
